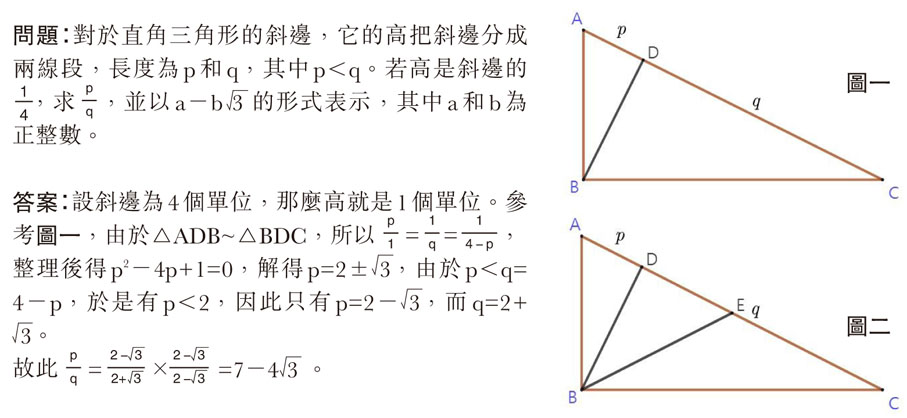
題解裏設斜邊為4個單位，那樣把q用p表示後，再發現了相似三角形關係，就找到了關於p的一元二次方程，之後留意到p較短，就找到了相應的q，然後找到兩者之比。

這裏要留意到，斜邊為4個單位，不是說4厘米之類的，題目所給圖形是沒有具體的長度單位的，可以放大縮小，形狀一樣，但大小有分別，最後的線段比，p：q是固定的。若果初接觸時，未看得通怎樣假設才不會影響計算，可以先設高為k，而斜邊為4k，計起來雖然多了個k，但最後還是能約去，答案是一樣的。

題目裏的資料中，留意到部分可以假設數字，化簡計算，而沒去引入許多代數，也是競賽題裏會接觸到的技巧之一。要是本身對題目的理解未能夠看清哪些可以假設，會導致做起來麻煩，又或者假設到計出來的結果可能跟原本資料有矛盾。

可利用直角三角形特性解題

這次談起直角三角形，也有點小特性，令這次的題目可以有個較特殊的解法。如圖二，設E為斜邊AC的中點，那樣有EB=EC=EA=2個單位，由於BD為1，於是由畢氏定理求得ED= 3，然後求得p，之後就解出答案了。

剛才EB，EC和EA相等這個小特性，要證明也很簡單，初中的幾何知識就夠了，通常是以課內習題形式出現，但應用起來挺方便，記住了是好的。

兩個解法比較起來，速度也沒什麼明顯的差別，大都是開闊了思路，令解起來多個思考角度。題目解法是多樣的，未必總能想得出一些特別好的方法，不過通常來說，想得久一點，多想出幾個解法，當中較好的方法會比較多。

其實平常日子裏，即便做很多數學題，也未必有什麼大發現，許多數學題，也不一定能看出什麼很有意思的想法。有時想出一點一滴的東西，值得記住的就只是那麼一點點而已。通常是累積得久了，許多基本的想法豐厚了，別人談些心得，才比較聽得懂，領悟起來多幾個具體例子可以參考，吸收各樣經驗也就容易些。

讀書思考的心得，有些書也會提及，只是若果自己思考的量未夠多，看著別人的心得就太抽象了，多數是明不了又用不了的。多數時候讀起這些書是有點迷惘，又一知半解，然後在平凡的日子裏，落些踏實的工夫，解難時多些反省什麼是優劣對錯，之後可能有天就會豁然開朗，一下子想法就連在一起，那時進步就大了。

● 張志基

簡介：奧校於1995年成立，為香港首間提供奧數培訓之註冊慈善機構(編號：91/4924)，每年均舉辦「香港小學數學奧林匹克比賽」，旨在發掘在數學方面有潛質的學生。學員有機會選拔成為香港代表隊，獲免費培訓並參加海內外重要大賽。詳情可瀏覽：www.hkmos.org。